Spickzettel: Definitionen und Erklärungen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{| class="mw-collapsible mw-collapsed wikitable" ! Was sind Funktionen? |- | Eindeutige Zuordnungen nennt man Funktion. Kostet eine Tafel Schokolade 1,50…“) |
|||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
|- | |- | ||
| | | | ||
| − | + | Eine eindeutige Zuordnung nennt man Funktion. | |
Kostet eine Tafel Schokolade 1,50€; 2 Tafeln Schokolade 3€, 3 Tafeln Schokolade 4,50€, so wird jeder Anzahl von Tafeln Schokolade ein Preis zugeordnet. | Kostet eine Tafel Schokolade 1,50€; 2 Tafeln Schokolade 3€, 3 Tafeln Schokolade 4,50€, so wird jeder Anzahl von Tafeln Schokolade ein Preis zugeordnet. | ||
| Zeile 10: | Zeile 10: | ||
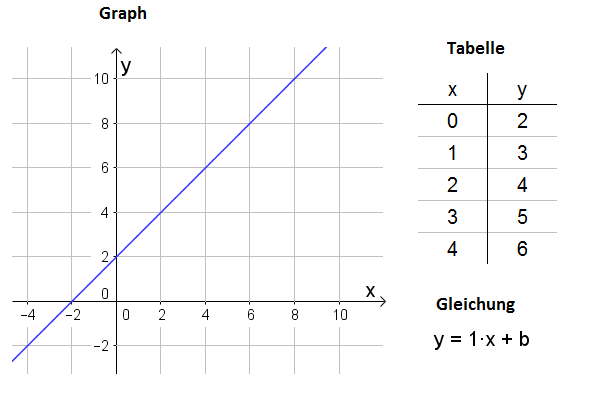
Funktionen kann man beispielsweise durch eine Funktionsgleichung, einen Graphen oder eine Tabelle darstellen. | Funktionen kann man beispielsweise durch eine Funktionsgleichung, einen Graphen oder eine Tabelle darstellen. | ||
| + | |||
| + | [[Datei:Spickzettel.png]] | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed wikitable" | ||
| + | ! Die Funktionsgleichung | ||
| + | |- | ||
| + | | | ||
| + | Häufig werden Funktionen als Funktionsgleichung dargestellt: | ||
| + | |||
| + | y = m*x + b | ||
| + | |||
| + | Dabei gibt m die Steigung an und b den "Startwert" (für x = 0) bzw. den y-Achsenabschnitt des Graphen an. | ||
| + | |||
| + | Möchte man einen Funktionswert berechnen so setzt man für x die entsprechende Zahl ein. | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed wikitable" | ||
| + | ! Was versteht man unter einer Steigung? | ||
| + | |- | ||
| + | | | ||
| + | Die Steigung gibt an, um wie viel eine Funktion zu- oder abnimmt, wenn man x um 1 erhöht. | ||
| + | |||
| + | In einem Graphen gibt sie an, wie steil eine Gerade verläuft und kann durch ein Steigungsdreieck dargestellt werden. | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed wikitable" | ||
| + | ! Was sind Lineare Funktionen? | ||
| + | |- | ||
| + | | | ||
| + | Lineare Funktionen werden über die Form ihrer Funktionsgleichung definiert: | ||
| + | |||
| + | y = m*x + b | ||
| + | |||
| + | Dabei bezeichnet m die Steigung und b den y-Achsenabschnitt. Für die beiden Variablen können beliebige Zahlen eingesetzt werden. | ||
|} | |} | ||
Aktuelle Version vom 18. November 2015, 18:09 Uhr
| Was sind Funktionen? |
|---|
|
Eine eindeutige Zuordnung nennt man Funktion. Kostet eine Tafel Schokolade 1,50€; 2 Tafeln Schokolade 3€, 3 Tafeln Schokolade 4,50€, so wird jeder Anzahl von Tafeln Schokolade ein Preis zugeordnet. Da jeder Anzahl immer nur eine Preis zugeordnet wird, nennt man diese Zuordnung eindeutig. Funktionen kann man beispielsweise durch eine Funktionsgleichung, einen Graphen oder eine Tabelle darstellen. |
| Die Funktionsgleichung |
|---|
|
Häufig werden Funktionen als Funktionsgleichung dargestellt: y = m*x + b Dabei gibt m die Steigung an und b den "Startwert" (für x = 0) bzw. den y-Achsenabschnitt des Graphen an. Möchte man einen Funktionswert berechnen so setzt man für x die entsprechende Zahl ein. |
| Was versteht man unter einer Steigung? |
|---|
|
Die Steigung gibt an, um wie viel eine Funktion zu- oder abnimmt, wenn man x um 1 erhöht. In einem Graphen gibt sie an, wie steil eine Gerade verläuft und kann durch ein Steigungsdreieck dargestellt werden. |
| Was sind Lineare Funktionen? |
|---|
|
Lineare Funktionen werden über die Form ihrer Funktionsgleichung definiert: y = m*x + b Dabei bezeichnet m die Steigung und b den y-Achsenabschnitt. Für die beiden Variablen können beliebige Zahlen eingesetzt werden. |